
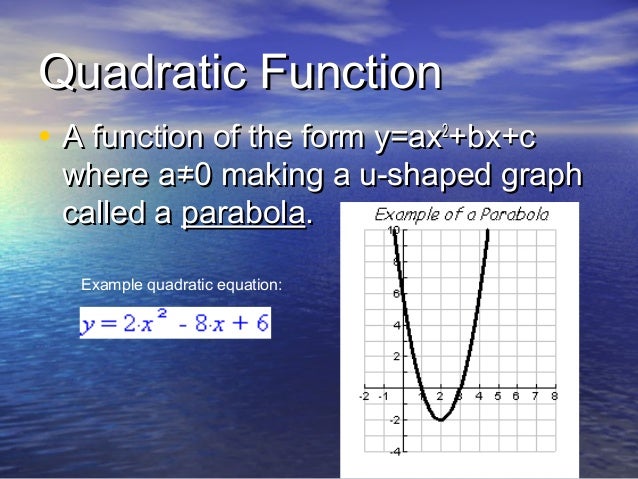
To find what the maximum revenue is, we can evaluate the revenue equation:Īs with any function, we can find the vertical intercepts of a quadratic by evaluating the function at an input of zero, and we can find the horizontal intercepts by solving for when the output will be zero. The idea is to use the coordinates of its vertex (maximum point, or minimum point) to write its. Helpful note: If your quadratics x-intercepts happen to be nice neat numbers (so theyre relatively easy to work with), a shortcut for finding the axis of symmetry is to note that this axis, this vertical line, is always exactly between the two x-intercepts.So you can just average the two intercepts to get the location of the axis of symmetry and the x-coordinate of the vertex.

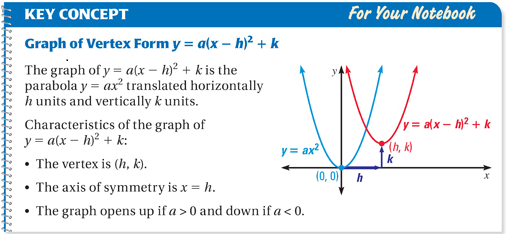
You can turn on tracing of the vertex to see how the vertex moves. We can use the vertex form to find a parabolas equation. The model tells us that the maximum revenue will occur if the newspaper charges $31.80 for a subscription. Also, shown is the form of the quadratic equation where are the coordinates of the vertex. H = − 80 2 ( − 2 ), k = A ( 20 ) = 80 ( 20 ) − 2 ( 20 ) 2 = 800 \displaystyle h = − 2 ( − 2, 500 ) 159, 000 = 31.8 I took the following steps to find the vertex: I divided every term by 5 to get a simplified equivalent function x 2 4 x + 3 Put it in the square form ( x 2 4 x + 4) 4 + 3 > ( x 2) 2 1 From the ( x 2) 2 1 form I would say the vertex coordinates are 2 -1, but I'm wrong.


 0 kommentar(er)
0 kommentar(er)
